Go to the source code of this file.
◆ cdli2()
| double complex function cdli2 |
( |
double complex |
z | ) |
|
Complex dilogarithm 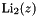 .
.
- Parameters
-
- Returns
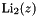
- Note
- Implementation translated from SPheno by Alexander Voigt
Definition at line 97 of file Li2.f90.
◆ dhorner()
| double precision function dhorner |
( |
double precision |
x, |
|
|
double precision, dimension(len) |
c, |
|
|
integer |
len |
|
) |
| |
Evaluation of polynomial P(x) with len coefficients c.
- Parameters
-
| x | real argument of P |
| c | coefficients of P(x) |
| len | number of coefficients |
- Returns
- P(x)
Definition at line 180 of file Li2.f90.
◆ dli2()
| double precision function dli2 |
( |
double precision |
x | ) |
|
Real dilogarithm 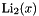 .
.
- Parameters
-
- Returns
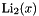
- Author
- Alexander Voigt
Implemented as an economized Pade approximation with a maximum error of 4.16e-18.
Definition at line 19 of file Li2.f90.
◆ fast_cdlog()
| double complex function fast_cdlog |
( |
double complex |
z | ) |
|
Fast implementation of complex logarithm.
- Parameters
-
- Returns
- log(z)
Definition at line 199 of file Li2.f90.
◆ li2c()
| subroutine li2c |
( |
double precision, intent(in) |
re_in, |
|
|
double precision, intent(in) |
im_in, |
|
|
double precision, intent(out) |
re_out, |
|
|
double precision, intent(out) |
im_out |
|
) |
| |
C wrapper for complex dilogarithm.
- Parameters
-
| re_in | real part of complex input |
| im_in | imaginary part of complex input |
| re_out | real part of complex output |
| im_out | imagoutary part of complex output |
- Returns
- log(z)
Definition at line 219 of file Li2.f90.
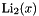 . More...
. More...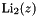 . More...
. More... 1.8.13
1.8.13