Namespaces
	CouplingOrders

	hierarchies

	mh2_eft

	mh2_fo

	mh2l

Classes
struct	Complex

struct	FlipSignOp

class	HierarchyCalculator

class	HierarchyObject

struct	Parameters

class	Temporarily_set

Typedefs
using	V2 = Eigen::Vector2d
	real 2-vector More...

using	RM22 = Eigen::Matrix2d
	real 2x2 matrix More...

using	CM22 = Eigen::Matrix2cd
	complex 2x2 matrix More...

using	CM44 = Eigen::Matrix4cd
	complex 4x4 matrix More...

using	RM33 = Eigen::Matrix3d
	real 3x3 matrix More...

using	RM44 = Eigen::Matrix4d
	real 4x4 matrix More...

Enumerations
enum	ELogLevel { kVerbose, kDebug, kInfo, kWarning, kError, kFatal }

Functions
std::ostream &	operator<< (std::ostream &ostr, const HierarchyObject &ho)

std::ostream &	operator<< (std::ostream &, const Parameters &)
	prints the Parameters struct to a stream More...

std::tuple< V2, V2, V2, V2 >	fs_diagonalize_hermitian_perturbatively (const RM22 &m0, const RM22 &m1, const RM22 &m2, const RM22 &m3)

template<class Real , class Scalar , int M, int N>
void	svd_eigen (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > u, Eigen::Matrix< Scalar, N, N > vh)

template<class Real , class Scalar , int N>
void	hermitian_eigen (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > *z)

template<int M, int N, class Real >
void	disna (const char &JOB, const Eigen::Array< Real, MIN_(M, N), 1 > &D, Eigen::Array< Real, MIN_(M, N), 1 > &SEP, int &INFO)

template<class Real , class Scalar , int M, int N>
void	svd_internal (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > u, Eigen::Matrix< Scalar, N, N > vh)

template<class Real , class Scalar , int M, int N>
void	svd_errbd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > u=0, Eigen::Matrix< Scalar, N, N > vh=0, Real s_errbd=0, Eigen::Array< Real, MIN_(M, N), 1 > u_errbd=0, Eigen::Array< Real, MIN_(M, N), 1 > *v_errbd=0)

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh)

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd)

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &u_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &v_errbd)

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s)

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Real &s_errbd)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian_internal (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > *z)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian_errbd (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > z=0, Real w_errbd=0, Eigen::Array< Real, N, 1 > *z_errbd=0)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd, Eigen::Array< Real, N, 1 > &z_errbd)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Real &w_errbd)

template<class Real , int N>
void	diagonalize_symmetric_errbd (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)

template<class Real , int N>
void	diagonalize_symmetric_errbd (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)

template<class Real , class Scalar , int M, int N>
void	reorder_svd_errbd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > u=0, Eigen::Matrix< Scalar, N, N > vh=0, Real s_errbd=0, Eigen::Array< Real, MIN_(M, N), 1 > u_errbd=0, Eigen::Array< Real, MIN_(M, N), 1 > *v_errbd=0)

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh)

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd)

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &u_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &v_errbd)

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s)

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Real &s_errbd)

template<class Real , int N>
void	reorder_diagonalize_symmetric_errbd (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , int N>
void	reorder_diagonalize_symmetric_errbd (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s)

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)

template<class Real , class Scalar , int M, int N>
void	fs_svd_errbd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > u=0, Eigen::Matrix< Scalar, N, N > v=0, Real s_errbd=0, Eigen::Array< Real, MIN_(M, N), 1 > u_errbd=0, Eigen::Array< Real, MIN_(M, N), 1 > *v_errbd=0)

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &v)

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &v, Real &s_errbd)

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &v, Real &s_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &u_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &v_errbd)

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s)

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Real &s_errbd)

template<class Real , int M, int N>
void	fs_svd (const Eigen::Matrix< Real, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< std::complex< Real >, M, M > &u, Eigen::Matrix< std::complex< Real >, N, N > &v)

template<class Real , int M, int N>
void	fs_svd (const Eigen::Matrix< Real, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< std::complex< Real >, M, M > &u, Eigen::Matrix< std::complex< Real >, N, N > &v, Real &s_errbd)

template<class Real , int M, int N>
void	fs_svd (const Eigen::Matrix< Real, M, N > &m, Eigen::Array< Real, MIN_(M, N), 1 > &s, Eigen::Matrix< std::complex< Real >, M, M > &u, Eigen::Matrix< std::complex< Real >, N, N > &v, Real &s_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &u_errbd, Eigen::Array< Real, MIN_(M, N), 1 > &v_errbd)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric_errbd (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian_errbd (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > z=0, Real w_errbd=0, Eigen::Array< Real, N, 1 > *z_errbd=0)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd, Eigen::Array< Real, N, 1 > &z_errbd)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Real &w_errbd)

double	li2 (double x)
	real dilogarithm from FORTRAN module More...

std::complex< double >	li2 (const std::complex< double > &z)
	complex dilogarithm from FORTRAN module More...

template<typename T >
Complex< T >	pos (const Complex< T > &z) noexcept
	converts -0.0 to 0.0 More...

template<typename T >
constexpr T	arg (const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	conj (const Complex< T > &z) noexcept

template<typename T >
Complex< T >	log (const Complex< T > &z_) noexcept

template<typename T >
constexpr T	norm_sqr (const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	operator+ (const Complex< T > &a, const Complex< T > &b) noexcept

template<typename T >
constexpr Complex< T >	operator+ (const Complex< T > &z, T x) noexcept

template<typename T >
constexpr Complex< T >	operator+ (T x, const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	operator- (const Complex< T > &a, const Complex< T > &b) noexcept

template<typename T >
constexpr Complex< T >	operator- (T x, const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	operator- (const Complex< T > &z, T x) noexcept

template<typename T >
constexpr Complex< T >	operator- (const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	operator* (const Complex< T > &a, const Complex< T > &b) noexcept

template<typename T >
constexpr Complex< T >	operator* (T x, const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	operator* (const Complex< T > &z, T x) noexcept

template<typename T >
constexpr Complex< T >	operator/ (T x, const Complex< T > &z) noexcept

template<typename T >
constexpr Complex< T >	operator/ (const Complex< T > &z, T x) noexcept

double	dilog (double x) noexcept
	Real dilogarithm 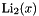$\mathrm{Li}_2(x)$ . More...

std::complex< double >	dilog (const std::complex< double > &z_) noexcept
	Complex dilogarithm 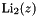$\mathrm{Li}_2(z)$ . More...

double	clausen_2 (double x) noexcept
	Clausen function 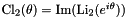$\mathrm{Cl}_2(\theta) = \mathrm{Im}(\mathrm{Li}_2(e^{i\theta}))$ . More...

Variables
static bool	isInfoPrinted
	if true, no info will be printed More...

const double	NaN = std::numeric_limits<double>::quiet_NaN()

Typedef Documentation

◆ CM22

using himalaya::CM22 = typedef Eigen::Matrix2cd

complex 2x2 matrix

Definition at line 22 of file Himalaya_interface.hpp.

◆ CM44

using himalaya::CM44 = typedef Eigen::Matrix4cd

complex 4x4 matrix

Definition at line 23 of file Himalaya_interface.hpp.

◆ RM22

typedef Eigen::Matrix2d himalaya::RM22

real 2x2 matrix

Definition at line 1521 of file Linalg.hpp.

◆ RM33

using himalaya::RM33 = typedef Eigen::Matrix3d

real 3x3 matrix

Definition at line 25 of file Himalaya_interface.hpp.

◆ RM44

using himalaya::RM44 = typedef Eigen::Matrix4d

real 4x4 matrix

Definition at line 26 of file Himalaya_interface.hpp.

◆ V2

typedef Eigen::Vector2d himalaya::V2

real 2-vector

Definition at line 1520 of file Linalg.hpp.

Enumeration Type Documentation

◆ ELogLevel

enum himalaya::ELogLevel

Enum representing the kind of output.

Enumerator
kVerbose
kDebug
kInfo
kWarning
kError
kFatal

Definition at line 45 of file Logger.hpp.

Function Documentation

◆ arg()

template<typename T >

constexpr T himalaya::arg ( const Complex< T > & z )

noexcept

Definition at line 33 of file complex.hpp.

◆ clausen_2()

double himalaya::clausen_2 ( double x )

noexcept

Clausen function $\mathrm{Cl}_2(\theta) = \mathrm{Im}(\mathrm{Li}_2(e^{i\theta}))$ .

Clausen function Cl_2(x)

Parameters

x	real angle

Returns: $\mathrm{Cl}_2(\theta)$

Definition at line 214 of file Li2.cpp.

◆ conj()

template<typename T >

constexpr Complex<T> himalaya::conj ( const Complex< T > & z )

noexcept

Definition at line 39 of file complex.hpp.

◆ diagonalize_hermitian() [1/5]

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z
	)

Diagonalizes N-by-N hermitian matrix m so that

m == z * w.matrix().asDiagonal() * z.adjoint()

Elements of w are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues
[out]	z	N-by-N unitary matrix

Definition at line 430 of file Linalg.hpp.

◆ diagonalize_hermitian() [2/5]

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd
	)

Same as diagonalize_hermitian(m, w, z) except that an approximate error bound for the eigenvalues is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of diagonalize_hermitian(m, w, z) for the other parameters.

Definition at line 450 of file Linalg.hpp.

◆ diagonalize_hermitian() [3/5]

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd,
		Eigen::Array< Real, N, 1 > &	z_errbd
	)

Same as diagonalize_hermitian(m, w, z, w_errbd) except that approximate error bounds for the eigenvectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] z_errbd array of approximate error bounds for z

See the documentation of diagonalize_hermitian(m, w, z, w_errbd) for the other parameters.

Definition at line 471 of file Linalg.hpp.

◆ diagonalize_hermitian() [4/5]

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w
	)

Returns eigenvalues of N-by-N hermitian matrix m via w. Elements of w are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues

Definition at line 492 of file Linalg.hpp.

◆ diagonalize_hermitian() [5/5]

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Real &	w_errbd
	)

Same as diagonalize_hermitian(m, w) except that an approximate error bound for the eigenvalues is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of diagonalize_hermitian(m, w) for the other parameters.

Definition at line 511 of file Linalg.hpp.

◆ diagonalize_hermitian_errbd()

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian_errbd	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z = `0`,
		Real *	w_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	z_errbd = `0`
	)

Definition at line 392 of file Linalg.hpp.

◆ diagonalize_hermitian_internal()

template<class Real , class Scalar , int N>

void himalaya::diagonalize_hermitian_internal	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z
	)

Definition at line 383 of file Linalg.hpp.

◆ diagonalize_symmetric() [1/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N complex symmetric matrix m so that

m == u * s.matrix().asDiagonal() * u.transpose()

and (s >= 0).all(). Elements of s are in descending order.

Template Parameters

Real	type of real and imaginary parts
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N complex symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Definition at line 551 of file Linalg.hpp.

◆ diagonalize_symmetric() [2/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 571 of file Linalg.hpp.

◆ diagonalize_symmetric() [3/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 592 of file Linalg.hpp.

◆ diagonalize_symmetric() [4/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N complex symmetric matrix m via s such that (s >= 0).all(). Elements of s are in descending order.

Template Parameters

Real	type of real and imaginary parts
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N complex symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Definition at line 612 of file Linalg.hpp.

◆ diagonalize_symmetric() [5/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s) for the other parameters.

Definition at line 631 of file Linalg.hpp.

◆ diagonalize_symmetric() [6/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N real symmetric matrix m so that

m == u * s.matrix().asDiagonal() * u.transpose()

and (s >= 0).all(). Order of elements of s is unspecified.

Template Parameters

Real	type of real and imaginary parts
N	number of rows and columns of m

Parameters

[in]	m	N-by-N real symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Note: Use diagonalize_hermitian() unless sign of s[i] matters.

Definition at line 679 of file Linalg.hpp.

◆ diagonalize_symmetric() [7/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 699 of file Linalg.hpp.

◆ diagonalize_symmetric() [8/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 720 of file Linalg.hpp.

◆ diagonalize_symmetric() [9/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N real symmetric matrix m via s such that (s >= 0).all(). Order of elements of s is unspecified.

Template Parameters

Real	type of elements of m and s
N	number of rows and columns of m

Parameters

[in]	m	N-by-N real symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Note: Use diagonalize_hermitian() unless sign of s[i] matters.

Definition at line 743 of file Linalg.hpp.

◆ diagonalize_symmetric() [10/10]

template<class Real , int N>

void himalaya::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s) for the other parameters.

Definition at line 762 of file Linalg.hpp.

◆ diagonalize_symmetric_errbd() [1/2]

template<class Real , int N>

void himalaya::diagonalize_symmetric_errbd	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 520 of file Linalg.hpp.

◆ diagonalize_symmetric_errbd() [2/2]

template<class Real , int N>

void himalaya::diagonalize_symmetric_errbd	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 648 of file Linalg.hpp.

◆ dilog() [1/2]

double himalaya::dilog ( double x )

noexcept

Real dilogarithm $\mathrm{Li}_2(x)$ .

real dilogarithm

Parameters

x	real argument

Returns: $\mathrm{Li}_2(x)$

Author: Alexander Voigt

Implemented as an economized Pade approximation with a maximum error of 4.16e-18.

Definition at line 62 of file Li2.cpp.

◆ dilog() [2/2]

std::complex< double > himalaya::dilog ( const std::complex< double > & z_ )

noexcept

Complex dilogarithm $\mathrm{Li}_2(z)$ .

complex dilogarithm

Parameters

z_	complex argument

Returns: $\mathrm{Li}_2(z)$

Note: Implementation translated from SPheno to C++

Author: Werner Porod

Note: translated to C++ by Alexander Voigt

Definition at line 141 of file Li2.cpp.

◆ disna()

template<int M, int N, class Real >

void himalaya::disna	(	const char &	JOB,
		const Eigen::Array< Real, MIN_(M, N), 1 > &	D,
		Eigen::Array< Real, MIN_(M, N), 1 > &	SEP,
		int &	INFO
	)

Template version of DDISNA from LAPACK.

Definition at line 74 of file Linalg.hpp.

◆ fs_diagonalize_hermitian() [1/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z
	)

Diagonalizes N-by-N hermitian matrix m so that

m == z.adjoint() * w.matrix().asDiagonal() * z    // convention of SARAH

w is arranged so that abs(w[i]) are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues
[out]	z	N-by-N unitary matrix

Definition at line 1432 of file Linalg.hpp.

◆ fs_diagonalize_hermitian() [2/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd
	)

Same as fs_diagonalize_hermitian(m, w, z) except that an approximate error bound for the eigenvalues is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of fs_diagonalize_hermitian(m, w, z) for the other parameters.

Definition at line 1452 of file Linalg.hpp.

◆ fs_diagonalize_hermitian() [3/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd,
		Eigen::Array< Real, N, 1 > &	z_errbd
	)

Same as fs_diagonalize_hermitian(m, w, z, w_errbd) except that approximate error bounds for the eigenvectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] z_errbd array of approximate error bounds for z

See the documentation of fs_diagonalize_hermitian(m, w, z, w_errbd) for the other parameters.

Definition at line 1473 of file Linalg.hpp.

◆ fs_diagonalize_hermitian() [4/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w
	)

Returns eigenvalues of N-by-N hermitian matrix m via w. w is arranged so that abs(w[i]) are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues

Definition at line 1494 of file Linalg.hpp.

◆ fs_diagonalize_hermitian() [5/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Real &	w_errbd
	)

Same as fs_diagonalize_hermitian(m, w) except that an approximate error bound for the eigenvalues is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of fs_diagonalize_hermitian(m, w) for the other parameters.

Definition at line 1513 of file Linalg.hpp.

◆ fs_diagonalize_hermitian_errbd()

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_hermitian_errbd	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z = `0`,
		Real *	w_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	z_errbd = `0`
	)

Definition at line 1393 of file Linalg.hpp.

◆ fs_diagonalize_hermitian_perturbatively()

std::tuple< V2, V2, V2, V2 > himalaya::fs_diagonalize_hermitian_perturbatively	(	const RM22 &	m0,
		const RM22 &	m1,
		const RM22 &	m2,
		const RM22 &	m3
	)

Diagonalizes a mass matrix perturbatively.

Parameters

m0	tree-level contribution
m1	1-loop contribution
m2	2-loop contribution
m3	3-loop contribution

Returns: perturbatively calculated mass eigenvalues

Diagonalizes a 2x2 hermitian mass matrix perturbatively.

Parameters

m0	tree-level contribution
m1	1-loop contribution
m2	2-loop contribution
m3	3-loop contribution

Returns: perturbatively calculated mass eigenvalues

Definition at line 46 of file Linalg.cpp.

◆ fs_diagonalize_symmetric() [1/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N symmetric matrix m so that

m == u.transpose() * s.matrix().asDiagonal() * u
// convention of Haber and Kane, Phys. Rept. 117 (1985) 75-263

and (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Definition at line 1303 of file Linalg.hpp.

◆ fs_diagonalize_symmetric() [2/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as fs_diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 1323 of file Linalg.hpp.

◆ fs_diagonalize_symmetric() [3/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as fs_diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of fs_diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 1344 of file Linalg.hpp.

◆ fs_diagonalize_symmetric() [4/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N symmetric matrix m via s such that (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Definition at line 1365 of file Linalg.hpp.

◆ fs_diagonalize_symmetric() [5/5]

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as fs_diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_diagonalize_symmetric(m, s) for the other parameters.

Definition at line 1384 of file Linalg.hpp.

◆ fs_diagonalize_symmetric_errbd()

template<class Real , class Scalar , int N>

void himalaya::fs_diagonalize_symmetric_errbd	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 1276 of file Linalg.hpp.

◆ fs_svd() [1/8]

template<class Real , class Scalar , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	v
	)

Singular value decomposition of M-by-N matrix m such that

sigma.setZero(); sigma.diagonal() = s;
m == u.transpose() * sigma * v
// convention of Haber and Kane, Phys. Rept. 117 (1985) 75-263

and (s >= 0).all(). Elements of s are in ascending order. The above decomposition can be put in the form

m == u.transpose() * s.matrix().asDiagonal() * v

if M == N.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and v
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M unitary matrix
[out]	v	N-by-N unitary matrix

Definition at line 1097 of file Linalg.hpp.

◆ fs_svd() [2/8]

template<class Real , class Scalar , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	v,
		Real &	s_errbd
	)

Same as fs_svd(m, s, u, v) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_svd(m, s, u, v) for the other parameters.

Definition at line 1118 of file Linalg.hpp.

◆ fs_svd() [3/8]

template<class Real , class Scalar , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	v,
		Real &	s_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	u_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	v_errbd
	)

Same as fs_svd(m, s, u, v, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of fs_svd(m, s, u, v, s_errbd) for the other parameters.

Definition at line 1141 of file Linalg.hpp.

◆ fs_svd() [4/8]

template<class Real , class Scalar , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s
	)

Returns singular values of M-by-N matrix m via s such that (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and v
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values

Definition at line 1165 of file Linalg.hpp.

◆ fs_svd() [5/8]

template<class Real , class Scalar , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Real &	s_errbd
	)

Same as fs_svd(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_svd(m, s) for the other parameters.

Definition at line 1183 of file Linalg.hpp.

◆ fs_svd() [6/8]

template<class Real , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Real, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< std::complex< Real >, M, M > &	u,
		Eigen::Matrix< std::complex< Real >, N, N > &	v
	)

Singular value decomposition of M-by-N real matrix m such that

sigma.setZero(); sigma.diagonal() = s;
m == u.transpose() * sigma * v
// convention of Haber and Kane, Phys. Rept. 117 (1985) 75-263

and (s >= 0).all(). Elements of s are in ascending order. The above decomposition can be put in the form

m == u.transpose() * s.matrix().asDiagonal() * v

if M == N.

Template Parameters

Real	type of real and imaginary parts
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N real matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M complex unitary matrix
[out]	v	N-by-N complex unitary matrix

Note: This is a convenience overload for the case where the type of u and v (complex) differs from that of m (real). Mathematically, real u and v are enough to accommodate SVD of any real m.

Definition at line 1218 of file Linalg.hpp.

◆ fs_svd() [7/8]

template<class Real , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Real, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< std::complex< Real >, M, M > &	u,
		Eigen::Matrix< std::complex< Real >, N, N > &	v,
		Real &	s_errbd
	)

Same as fs_svd(m, s, u, v) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_svd(m, s, u, v) for the other parameters.

Definition at line 1239 of file Linalg.hpp.

◆ fs_svd() [8/8]

template<class Real , int M, int N>

void himalaya::fs_svd	(	const Eigen::Matrix< Real, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< std::complex< Real >, M, M > &	u,
		Eigen::Matrix< std::complex< Real >, N, N > &	v,
		Real &	s_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	u_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	v_errbd
	)

Same as fs_svd(m, s, u, v, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of fs_svd(m, s, u, v, s_errbd) for the other parameters.

Definition at line 1262 of file Linalg.hpp.

◆ fs_svd_errbd()

template<class Real , class Scalar , int M, int N>

void himalaya::fs_svd_errbd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u = `0`,
		Eigen::Matrix< Scalar, N, N > *	v = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, MIN_(M, N), 1 > *	u_errbd = `0`,
		Eigen::Array< Real, MIN_(M, N), 1 > *	v_errbd = `0`
	)

Definition at line 1060 of file Linalg.hpp.

◆ hermitian_eigen()

template<class Real , class Scalar , int N>

void himalaya::hermitian_eigen	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z
	)

Definition at line 60 of file Linalg.hpp.

◆ li2() [1/2]

double himalaya::li2 ( double x )

real dilogarithm from FORTRAN module

Definition at line 17 of file Li2f.cpp.

◆ li2() [2/2]

std::complex< double > himalaya::li2 ( const std::complex< double > & z )

complex dilogarithm from FORTRAN module

Definition at line 24 of file Li2f.cpp.

◆ log()

template<typename T >

Complex<T> himalaya::log ( const Complex< T > & z_ )

noexcept

Definition at line 45 of file complex.hpp.

◆ norm_sqr()

template<typename T >

constexpr T himalaya::norm_sqr ( const Complex< T > & z )

noexcept

Definition at line 52 of file complex.hpp.

◆ operator*() [1/3]

template<typename T >

constexpr Complex<T> himalaya::operator*	(	const Complex< T > &	a,
		const Complex< T > &	b
	)

noexcept

Definition at line 100 of file complex.hpp.

◆ operator*() [2/3]

template<typename T >

constexpr Complex<T> himalaya::operator*	(	T	x,
		const Complex< T > &	z
	)

noexcept

Definition at line 106 of file complex.hpp.

◆ operator*() [3/3]

template<typename T >

constexpr Complex<T> himalaya::operator*	(	const Complex< T > &	z,
		T	x
	)

noexcept

Definition at line 112 of file complex.hpp.

◆ operator+() [1/3]

template<typename T >

constexpr Complex<T> himalaya::operator+	(	const Complex< T > &	a,
		const Complex< T > &	b
	)

noexcept

Definition at line 58 of file complex.hpp.

◆ operator+() [2/3]

template<typename T >

constexpr Complex<T> himalaya::operator+	(	const Complex< T > &	z,
		T	x
	)

noexcept

Definition at line 64 of file complex.hpp.

◆ operator+() [3/3]

template<typename T >

constexpr Complex<T> himalaya::operator+	(	T	x,
		const Complex< T > &	z
	)

noexcept

Definition at line 70 of file complex.hpp.

◆ operator-() [1/4]

template<typename T >

constexpr Complex<T> himalaya::operator-	(	const Complex< T > &	a,
		const Complex< T > &	b
	)

noexcept

Definition at line 76 of file complex.hpp.

◆ operator-() [2/4]

template<typename T >

constexpr Complex<T> himalaya::operator-	(	T	x,
		const Complex< T > &	z
	)

noexcept

Definition at line 82 of file complex.hpp.

◆ operator-() [3/4]

template<typename T >

constexpr Complex<T> himalaya::operator-	(	const Complex< T > &	z,
		T	x
	)

noexcept

Definition at line 88 of file complex.hpp.

◆ operator-() [4/4]

template<typename T >

constexpr Complex<T> himalaya::operator- ( const Complex< T > & z )

noexcept

Definition at line 94 of file complex.hpp.

◆ operator/() [1/2]

template<typename T >

constexpr Complex<T> himalaya::operator/	(	T	x,
		const Complex< T > &	z
	)

noexcept

Definition at line 118 of file complex.hpp.

◆ operator/() [2/2]

template<typename T >

constexpr Complex<T> himalaya::operator/	(	const Complex< T > &	z,
		T	x
	)

noexcept

Definition at line 124 of file complex.hpp.

◆ operator<<() [1/2]

std::ostream & himalaya::operator<<	(	std::ostream &	ostr,
		const Parameters &	pars
	)

prints the Parameters struct to a stream

Definition at line 263 of file Himalaya_interface.cpp.

◆ operator<<() [2/2]

std::ostream & himalaya::operator<<	(	std::ostream &	ostr,
		const HierarchyObject &	ho
	)

Prints out all information of the HierarchyObject

Definition at line 573 of file HierarchyObject.cpp.

◆ pos()

template<typename T >

Complex<T> himalaya::pos ( const Complex< T > & z )

noexcept

converts -0.0 to 0.0

Definition at line 25 of file complex.hpp.

◆ reorder_diagonalize_symmetric() [1/5]

template<class Real , class Scalar , int N>

void himalaya::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N symmetric matrix m so that

m == u * s.matrix().asDiagonal() * u.transpose()

and (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Definition at line 970 of file Linalg.hpp.

◆ reorder_diagonalize_symmetric() [2/5]

template<class Real , class Scalar , int N>

void himalaya::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as reorder_diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 990 of file Linalg.hpp.

◆ reorder_diagonalize_symmetric() [3/5]

template<class Real , class Scalar , int N>

void himalaya::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as reorder_diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of reorder_diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 1011 of file Linalg.hpp.

◆ reorder_diagonalize_symmetric() [4/5]

template<class Real , class Scalar , int N>

void himalaya::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N symmetric matrix m via s such that (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Definition at line 1032 of file Linalg.hpp.

◆ reorder_diagonalize_symmetric() [5/5]

template<class Real , class Scalar , int N>

void himalaya::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as reorder_diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_diagonalize_symmetric(m, s) for the other parameters.

Definition at line 1051 of file Linalg.hpp.

◆ reorder_diagonalize_symmetric_errbd() [1/2]

template<class Real , int N>

void himalaya::reorder_diagonalize_symmetric_errbd	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 917 of file Linalg.hpp.

◆ reorder_diagonalize_symmetric_errbd() [2/2]

template<class Real , int N>

void himalaya::reorder_diagonalize_symmetric_errbd	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 931 of file Linalg.hpp.

◆ reorder_svd() [1/5]

template<class Real , class Scalar , int M, int N>

void himalaya::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh
	)

Singular value decomposition of M-by-N matrix m such that

sigma.setZero(); sigma.diagonal() = s;
m == u * sigma * vh    // LAPACK convention

and (s >= 0).all(). Elements of s are in ascending order. The above decomposition can be put in the form

m == u * s.matrix().asDiagonal() * vh

if M == N.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M unitary matrix
[out]	vh	N-by-N unitary matrix

Definition at line 821 of file Linalg.hpp.

◆ reorder_svd() [2/5]

template<class Real , class Scalar , int M, int N>

void himalaya::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd
	)

Same as reorder_svd(m, s, u, vh) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_svd(m, s, u, vh) for the other parameters.

Definition at line 842 of file Linalg.hpp.

◆ reorder_svd() [3/5]

template<class Real , class Scalar , int M, int N>

void himalaya::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	u_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	v_errbd
	)

Same as reorder_svd(m, s, u, vh, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of reorder_svd(m, s, u, vh, s_errbd) for the other parameters.

Definition at line 865 of file Linalg.hpp.

◆ reorder_svd() [4/5]

template<class Real , class Scalar , int M, int N>

void himalaya::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s
	)

Returns singular values of M-by-N matrix m via s such that (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values

Definition at line 889 of file Linalg.hpp.

◆ reorder_svd() [5/5]

template<class Real , class Scalar , int M, int N>

void himalaya::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Real &	s_errbd
	)

Same as reorder_svd(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_svd(m, s) for the other parameters.

Definition at line 908 of file Linalg.hpp.

◆ reorder_svd_errbd()

template<class Real , class Scalar , int M, int N>

void himalaya::reorder_svd_errbd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u = `0`,
		Eigen::Matrix< Scalar, N, N > *	vh = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, MIN_(M, N), 1 > *	u_errbd = `0`,
		Eigen::Array< Real, MIN_(M, N), 1 > *	v_errbd = `0`
	)

Definition at line 771 of file Linalg.hpp.

◆ svd() [1/5]

template<class Real , class Scalar , int M, int N>

void himalaya::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh
	)

Singular value decomposition of M-by-N matrix m such that

sigma.setZero(); sigma.diagonal() = s;
m == u * sigma * vh    // LAPACK convention

and (s >= 0).all(). Elements of s are in descending order. The above decomposition can be put in the form

m == u * s.matrix().asDiagonal() * vh

if M == N.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M unitary matrix
[out]	vh	N-by-N unitary matrix

Definition at line 287 of file Linalg.hpp.

◆ svd() [2/5]

template<class Real , class Scalar , int M, int N>

void himalaya::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd
	)

Same as svd(m, s, u, vh) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of svd(m, s, u, vh) for the other parameters.

Definition at line 307 of file Linalg.hpp.

◆ svd() [3/5]

template<class Real , class Scalar , int M, int N>

void himalaya::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	u_errbd,
		Eigen::Array< Real, MIN_(M, N), 1 > &	v_errbd
	)

Same as svd(m, s, u, vh, s_errbd) except that approximate error bounds for the singular vectors are returned as well. The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of svd(m, s, u, vh, s_errbd) for the other parameters.

Definition at line 330 of file Linalg.hpp.

◆ svd() [4/5]

template<class Real , class Scalar , int M, int N>

void himalaya::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s
	)

Returns singular values of M-by-N matrix m via s such that (s >= 0).all(). Elements of s are in descending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values

Definition at line 354 of file Linalg.hpp.

◆ svd() [5/5]

template<class Real , class Scalar , int M, int N>

void himalaya::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Real &	s_errbd
	)

Same as svd(m, s) except that an approximate error bound for the singular values is returned as well. The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of svd(m, s) for the other parameters.

Definition at line 372 of file Linalg.hpp.

◆ svd_eigen()

template<class Real , class Scalar , int M, int N>

void himalaya::svd_eigen	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u,
		Eigen::Matrix< Scalar, N, N > *	vh
	)

Definition at line 46 of file Linalg.hpp.

◆ svd_errbd()

template<class Real , class Scalar , int M, int N>

void himalaya::svd_errbd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u = `0`,
		Eigen::Matrix< Scalar, N, N > *	vh = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, MIN_(M, N), 1 > *	u_errbd = `0`,
		Eigen::Array< Real, MIN_(M, N), 1 > *	v_errbd = `0`
	)

Definition at line 234 of file Linalg.hpp.

◆ svd_internal()

template<class Real , class Scalar , int M, int N>

void himalaya::svd_internal	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real, MIN_(M, N), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u,
		Eigen::Matrix< Scalar, N, N > *	vh
	)

Definition at line 178 of file Linalg.hpp.

Variable Documentation

◆ isInfoPrinted

bool himalaya::isInfoPrinted

static

if true, no info will be printed

Definition at line 42 of file HierarchyCalculator.cpp.

◆ NaN

const double himalaya::NaN = std::numeric_limits<double>::quiet_NaN()

Definition at line 27 of file Himalaya_interface.hpp.

Namespaces

Classes

Typedefs

Enumerations

Functions

Variables

Typedef Documentation

◆ CM22

◆ CM44

◆ RM22

◆ RM33

◆ RM44

◆ V2

Enumeration Type Documentation

◆ ELogLevel

Function Documentation

◆ arg()

◆ clausen_2()

◆ conj()

◆ diagonalize_hermitian() [1/5]

◆ diagonalize_hermitian() [2/5]

◆ diagonalize_hermitian() [3/5]

◆ diagonalize_hermitian() [4/5]

◆ diagonalize_hermitian() [5/5]

◆ diagonalize_hermitian_errbd()

◆ diagonalize_hermitian_internal()

◆ diagonalize_symmetric() [1/10]

◆ diagonalize_symmetric() [2/10]

◆ diagonalize_symmetric() [3/10]

◆ diagonalize_symmetric() [4/10]

◆ diagonalize_symmetric() [5/10]

◆ diagonalize_symmetric() [6/10]

◆ diagonalize_symmetric() [7/10]

◆ diagonalize_symmetric() [8/10]

◆ diagonalize_symmetric() [9/10]

◆ diagonalize_symmetric() [10/10]

◆ diagonalize_symmetric_errbd() [1/2]

◆ diagonalize_symmetric_errbd() [2/2]

◆ dilog() [1/2]

◆ dilog() [2/2]

◆ disna()

◆ fs_diagonalize_hermitian() [1/5]

◆ fs_diagonalize_hermitian() [2/5]

◆ fs_diagonalize_hermitian() [3/5]

◆ fs_diagonalize_hermitian() [4/5]

◆ fs_diagonalize_hermitian() [5/5]

◆ fs_diagonalize_hermitian_errbd()

◆ fs_diagonalize_hermitian_perturbatively()

◆ fs_diagonalize_symmetric() [1/5]

◆ fs_diagonalize_symmetric() [2/5]

◆ fs_diagonalize_symmetric() [3/5]

◆ fs_diagonalize_symmetric() [4/5]

◆ fs_diagonalize_symmetric() [5/5]

◆ fs_diagonalize_symmetric_errbd()

◆ fs_svd() [1/8]

◆ fs_svd() [2/8]

◆ fs_svd() [3/8]

◆ fs_svd() [4/8]

◆ fs_svd() [5/8]

◆ fs_svd() [6/8]

◆ fs_svd() [7/8]

◆ fs_svd() [8/8]

◆ fs_svd_errbd()

◆ hermitian_eigen()

◆ li2() [1/2]

◆ li2() [2/2]

◆ log()

◆ norm_sqr()

◆ operator*() [1/3]

◆ operator*() [2/3]

◆ operator*() [3/3]

◆ operator+() [1/3]

◆ operator+() [2/3]

◆ operator+() [3/3]

◆ operator-() [1/4]

◆ operator-() [2/4]

◆ operator-() [3/4]

◆ operator-() [4/4]

◆ operator/() [1/2]

◆ operator/() [2/2]